Question

A 150 foot tall monument is located in the distance. from a window in the building, a person determines that the angle of elevation to the top of the monument is 11° and that the angle of depression to the bottom of the monument is 8°. how far is the person from the monument? (round your answer to four decimal places)

Answer 1

Let's draw the problem:

As we can see, we have a pair of right triangles, and for both the distance we want if the adjacent leg with respect to the known angles. The opposite legs add up to the monument heigh.

So, we can use tangent of each angle to find the portion of the height and add them:

`\begin{gathered} \tan 11\degree=(h_1)/(d) \\ h_1=d\tan 11\degree \end{gathered}`
`\begin{gathered} \tan 8\degree=(h_2)/(d) \\ h_2=d\tan 8\degree \end{gathered}`

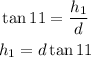
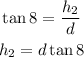
Since h1 and h2 add to 150 ft, we have:

`\begin{gathered} h_1+h_2=150 \\ d\tan 11\degree+d\tan 8\degree=150 \\ d(\tan 11\degree+\tan 8\degree)=150 \\ d=(150)/((\tan 11\degree+\tan 8\degree)) \\ d=(150)/(0.19438\ldots+0.14054\ldots)=(150)/(0.334921\ldots)\approx447.8666 \end{gathered}`

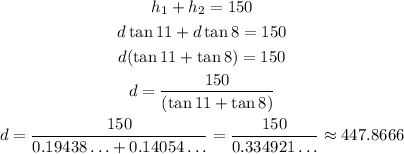
So, the distance is 447.8666 ft.