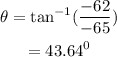Question

Ruth sets out to visit her friend Ward, who lives 50 mi north and 100 east of her. She starts by driving east but after 30 mi she comes to a detour that takes her 15 I south before going east again. She then drives east for 8 mi and runs out of gas, so Ward flies there in a small plane to get her. What is Wards displacement vector? Give your answer a() in component form, using a coordinate system in which the y axis points north and (b) as a magnitude and direction.

Answer 1

(A)

Consider the Ruths home as origin, then at wards home, position vector is given as

`x_1=100i+50j`

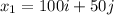
The above equation is written because from the given data, she lives 100miles east of her which is on the positive x-axis and 50 miles north which is on the positive y-axis.

At Ruth's home, the position vector is given as

`x_2=38i-15j`

The above equation is written because she is moving closer to the positive x-axis in 30 miles after which she also flew east in 8 miles. Also, she went south in 15 miles which is down the negative y-axis.

The Ward's displacement vector is calculated as

`\begin{gathered} x=x_2-x_1 \\ =(38i-15j)-(100i+50j) \\ =-62i-65j \end{gathered}`

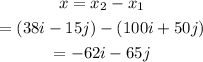
In component form, it can be written as

`x=(-62,-65)`

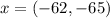
(b)

The magnitude of Ward's displacement vector is calculated as

`\begin{gathered} \lvert x\rvert=\sqrt[]{(-62)^2+(-65)^2} \\ =89.82\text{ m} \\ \approx90\text{ m} \end{gathered}`

Hence, the magnitude of Ward's displacement vector is 90 m

The direction of Ward's displacement vector is calculated as

`\begin{gathered} \theta=\tan ^(-1)((-62)/(-65)) \\ =43.64^0 \end{gathered}`