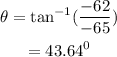(A)
Consider the Ruths home as origin, then at wards home, position vector is given as
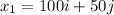
The above equation is written because from the given data, she lives 100miles east of her which is on the positive x-axis and 50 miles north which is on the positive y-axis.
At Ruth's home, the position vector is given as
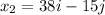
The above equation is written because she is moving closer to the positive x-axis in 30 miles after which she also flew east in 8 miles. Also, she went south in 15 miles which is down the negative y-axis.
The Ward's displacement vector is calculated as
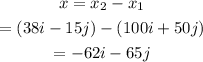
In component form, it can be written as
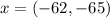
(b)
The magnitude of Ward's displacement vector is calculated as
![\begin{gathered} \lvert x\rvert=\sqrt[]{(-62)^2+(-65)^2} \\ =89.82\text{ m} \\ \approx90\text{ m} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/uojeqswhw5t8vf7u7kd8.png)
Hence, the magnitude of Ward's displacement vector is 90 m
The direction of Ward's displacement vector is calculated as