Answer:
Solution set of the quadratic equation is, Empty set
Explanation:
Given the quadratic equation:

Subtraction property of equality states that you subtract the same number to both sides of an equation.
Subtract both sides by 1 we get;
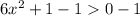
Simplify:
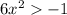
Division property of equality states that you divide the same number to both sides of an equation.
Divide both sides by 6 we get;
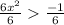
Simplify:
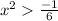
For any x in real number there does not exist any number x which satisfy
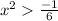 , therefore, there is no solution for this set of the quadratic inequality or in other word we can say that set of the solution is Empty set.
, therefore, there is no solution for this set of the quadratic inequality or in other word we can say that set of the solution is Empty set.