Step 1
Plot the graph of the data provided
Step 2
Find the class for the r-value for this data.
The r-value for this data based on the plot = 0.8482
Step 3
Find the classification of the correlation.
An r-value of 0.8482 is classified as a strong uphill(positive) linear relationship. This shows that there is a strong positive correlation or relationship between the height and weight data given.
Step 3
Find the linear equation for the given data.

Step 4
Based on this trend, a 6-foot-9 person will weigh?
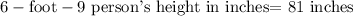
Substitute 81 inches into the equation

Hence, a 6-foot-9 person will weigh approximately 268 pounds.
Step 5
Based on this trend, a 303-pounds person's height will be?
Substitute 303lb into the equation
![\begin{gathered} 303=4.99642x-136.565 \\ 303+136.565=4.99642x \\ (4.99642x)/(4.99642)=(439.565)/(4.99642) \\ x=87.97599081 \\ x\approx88\operatorname{cm} \end{gathered}]()
Hence, the height of a 303-pound will be approximately 88cm