We are asked to determine the force required to stop a car that is moving at a velocity of 91.3 km/h.
First, we will convert the 91.3 km/h into m/s. To do that we will use the following conversion factors:
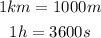
Multiplying the conversion factors we get:
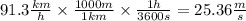
Now. We use a balance of energy. The work done by the force to stop the car must be equal to the change in kinetic energy of the car, therefore, we have:
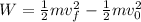
Since the car will stop this means that the final velocity is 0:
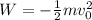
The work done is equal to the product of the force and the distance:
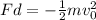
Now, we divide both sides by the distance "d":
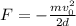
Substituting the values:
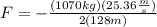
Solving the operations:
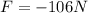
Therefore, the magnitude of the force required is 106 Newtons.