Answer:
The automobile is running at speed of 23.806 meters per second.
Step-by-step explanation:
From Kinematic we remember that acceleration (
 ) can be defined by this ordinary differential equation in terms of distance:
) can be defined by this ordinary differential equation in terms of distance:
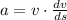 (1)
(1)
Where:
 - Speed of the automobile, measured in meters per second.
- Speed of the automobile, measured in meters per second.
 - Distance travelled by the automobile, measured in meters.
- Distance travelled by the automobile, measured in meters.
If we know that
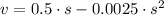 , then the equation of acceleration is:
, then the equation of acceleration is:
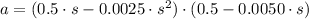
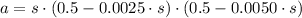
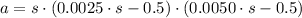
But distance covered by the vehicle is defined by the following formula:
 (2)
(2)
Where:
 - Arc angle, measured in radians.
- Arc angle, measured in radians.
 - Radius, measured in radians.
- Radius, measured in radians.
Then, we expand (1) by means of this result:
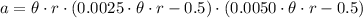

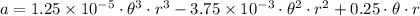
And finally we get the following third order polynomial:
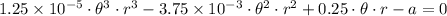 (3)
(3)
If we know that
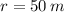 ,
,
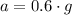 and
and
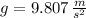 , then the polynomial becomes into this:
, then the polynomial becomes into this:
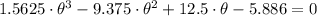 (3b)
(3b)
This polynomial can be solved analytically by Cardano's Method or by numerical methods. The roots of the polynomial are, respectivelly:
 ,
,
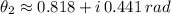 ,
,
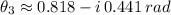 ,
,
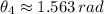
Both first and fourth roots are physically reasonable solution, but the latter represents the angle where automobile begins to skid first. Then, the automobile begins to skid at an angle of 1.563 radians relative to x axis.
The distance travelled by the automobile is: (
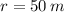 ,
,
 )
)
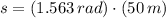

Lastly, the speed of the automobile at this location is: (
 )
)
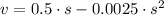 (4)
(4)

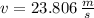
The automobile is running at speed of 23.806 meters per second.