Question

Factor completely: 8x^9 y^6 z^6 + 40x^8 y^3 z^6

Answer 1

`8x^9y^6z^6+40x^8y^3z^8`

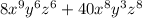
8*x^9*y^6*z^6 + 40*x^8*y^3*z^8

In order to factor this expression we need to find the common factor between the two terms. First we need to find the largest common factor between the two numerical parts, in this case 8 and 40. In this case, we can divide 40 by 8 directly, therefore the common factor is 8. For the variables we need to find the largest common factor aswell and to do this we need to indentify the letters that are repeated and between them the factor we are looking for is the one with the smallest expoent.

The "x" variable is repeated in both terms, the first one appears as x^9 while the second one is x^8. So the common factor is x^8.

The y variable is repeated in both terms, the first one appears as y^6 while the second one appears as y^3. So the common factor is y^3.

Lastly the z variable appears in both terms, with the first one being z^6 and the second z^8. So the common factor is z^6.

We now take all the common factors and divide each term by them as shown below:

`8\cdot x^8\cdot y^3\cdot z^6(x^{}\cdot y^3+5\cdot z^2)`

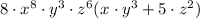
The result is 8*x^8*y^3*z^6*(x*y^3 + 5*z^2).