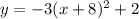Question

Suppose a parabola has an axis of symmetry at x=-8, a maximum height of 2, and passes through the point (-7,-1). Write the equation of the parabola in vertex form.

Answer 1

Y=-3(x+8)^2+2 Fill in the vertex (-8,2), and the ordered pair(-7.1) then solve for a. Y = a(x-h)^2 + k

Answer 2

we know that

If an axis of symmetry is
`x=-8` and has a maximum height of
`2`

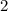
then

Is a vertical parabola open down with vertex at
`(-8,2)`

the equation in vertex form is equal to

`y=a(x-h)^(2)+k`

where

(h,k) is the vertex

substitute

`y=a(x+8)^(2)+2`

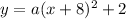
Find the value of a

the parabola passes through the point
`(-7,-1)`

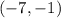
substitute in the formula

`-1=a(-7+8)^(2)+2`

`-1=a(1)^(2)+2`

`-1=a+2`

`a=-3`

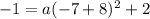
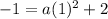
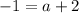
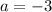
therefore

the answer is

the equation in vertex form is
`y=-3(x+8)^(2)+2`