Question

The playing field for a particular sport is a rectangle whose length is 5 feet more than twice the width. The perimeter of the playing field is 238 feet. Find the dimensions of the playing field.

Answer 1

To solve this problem we need to use a system of equations.

The first equation will be the one that is described in the first part of the problem, the length is 5 feet more than twice the width:

`l=2w+5`

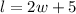
The second is the one that is related to the perimeter. We know that the perimeter of a rectangle is twice the length plus twice the width, it means:

`2l+2w=238`

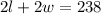
We can use these equation to find the dimensions of the playing field. For example, we can use the first equation to replace l in the second equation and then solve for w:

`\begin{gathered} 2(2w+5)+2w=238 \\ 4w+10+2w=238 \\ 6w+10=238 \\ 6w=238-10 \\ 6w=228 \\ w=(228)/(6) \\ w=38 \end{gathered}`

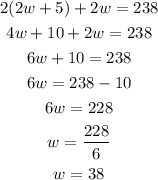
The width of the field is 38. Use this value to find the length:

`\begin{gathered} l=2w+5 \\ l=2(38)+5 \\ l=76+5 \\ l=81 \end{gathered}`

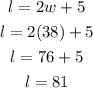
The length of the field is 81.

The dimensions of the field are 38 and 81.