he standard form of a quadratic efunctionis:
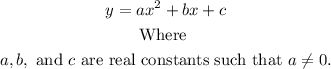
Since the y-intercept is (0, -1.4), it follows that:
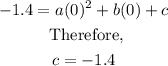
Substitute c = -1.4 into the equation:
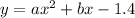
Since the x-intercept is (0.905, 0), it follows that:
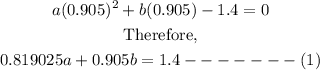
Since the graph passes through the third point (2, 0.6), it follows that:

Substitute equation (2) into equation (1):

Substitute a = -0.5 into equation (2), therefore,
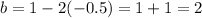
Therfore the function is given by:
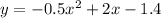
The equation of the parabola is y = -0.5x² + 2x - 1.4
.