Question

HS. Algebra 2A [M] (Prescriptive) (GP)11. Solve x4 + 3x2 - 4 = 0.*= tv2 or x = Eix = +2 or x =Ox = ti or x = 32x = +2i or x = +1

Answer 1

The given equation is,

`x^4+3x^2-4=0\ldots\ldots.(1)`

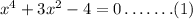
Let

`y=x^2`

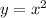
Then, equation (1) becomes,

`y^2+3y-4=0\ldots\ldots..(2)`

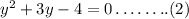
The general form of a quadratic equation can be written as,

`ay^2+by+c=0\ldots\ldots..(3)`

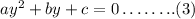
Comparing equations (2) and (3), we get a=1, b=3 and c=-4.

Hence, the solution for equation (2) can be calculated using discriminant method as

`\begin{gathered} y=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ y=\frac{-3\pm\sqrt[]{3^2-4*1*(-4)}}{2*1} \\ y=\frac{-3\pm\sqrt[]{9+16}}{2} \\ y=\frac{-3\pm\sqrt[]{25}}{2} \\ y=(-3\pm5)/(2) \\ y=(-3+5)/(2)\text{ or y=}(-3-5)/(2) \\ y=(2)/(2)\text{ or }y=(-8)/(2) \\ y=1\text{ or }y=-4 \end{gathered}`

We had defined y as,

`x^2=y\ldots\ldots(4)`

Put y=1 and y=-4 in the above equation to find the values of x.

Putting y=1,

`\begin{gathered} x^2=1 \\ x=\pm\sqrt[]{1} \\ x=\pm1 \end{gathered}`

Putting y=-4 in equation (4),

`\begin{gathered} x^2=-4 \\ x=\pm\sqrt[]{-4} \\ x=\pm\sqrt[]{-1*4} \\ x=\pm2*\sqrt[]{-1} \\ As\text{ }\sqrt[]{-1}=i, \\ x=\pm2i \end{gathered}`