Question

A car has a mass of 1500 kg. If the driver applies the brakes while on a gravel road, the maximum friction force that the tires can provide without skidding is about 7000 N. how long are the skid marks

Answer 1

Step-by-step explanation:

Given data:

mass of the car = 1500 kg

maximum friction force = 7000 N

initial velocity v_i = 20 m/s ( it is not given in the question just an assumption)

final velocity v_f = 0 m/s

`\begin{array}{l}</p><p>\sum F_(y)=M g-F_(n)=0 \\</p><p>\sum F_(x)=-F_(s)=m a_(x) \\</p><p>-F_(s)=m a_(x)</p><p>\end{array}`

`a_(x)=(-F_(s))/(m)=(-7000)/(1500)`

`a_(x)=-4.7 \mathrm{~m} / \mathrm{s}^(2)`

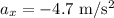
Now we can find the distance from this formula:

`v_(f x)^(2)=v_(i x)^(2)+2 a_(x)(\Delta x)`

`0=20^(2)+(2 *-4.7 * \Delta x)`

`20^(2)=9.4 \Delta x`

`\Delta x=(20^(2))/(9.4)=42.55 \mathrm{~m}`

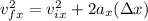
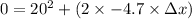
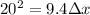
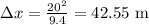
So, the shortest distance in which the car can stop safely without kidding

=42.55 m