1) In this problem, let's consider that there was no other investment after the initial investment of $30,000. Since the interest rate of this investment will be compounded annually, we can write the following below:
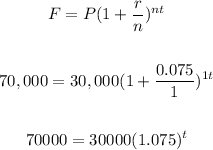
2) Now, we can solve for "t" applying logarithms:
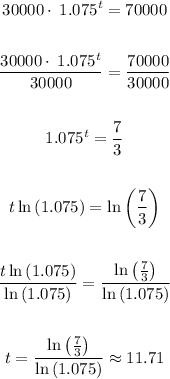
3) So, you have to wait almost 12 years (11.7) so that the investmente reaches