Question

In the figure below, points J, K, and L are the midpoints of the sides of Triangle XYZ. Suppose Xz=28, kl=42, and us=76 find the following lengths

Answer 1

We have one triangle inside another, of which the vertices of the smaller triangle are the midpoints of the sides of the bigger triangle.

We know the lengths of the sides: XZ = 28, KL = 42 and YZ = 76.

We can construct similar triangles, like YLJ and YZK.

Knowing that L is the midpoint of YZ, we know that YL = (1/2)*YZ. Then, the sides of YLJ are half the length of their corresponding sides of YZK.

In the same way we can relate each corresponding side as:

• LK is half as long as XY.

,

• LJ is half as long as XZ.

,

• KJ is half as long as YZ

Then, we can start by calculating XY.

As this side is the double of LK, its length is:

`XY=2\cdot LK=2\cdot42=84`

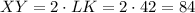
We continue with JY.

JY is half segment of XY, so its length is 42.

Finally, JK is half the length of YZ, so its length is:

`JK=(1)/(2)\cdot YZ=(1)/(2)\cdot76=38`

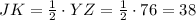
Answer:

XY = 84

JY = 42

JK = 38