Answer:
length = 26 ft
width = 26 ft
Step-by-step explanation:
The length of the rectangle is 4 less than 2 times the width:
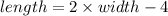
The perimeter of the rectangle is 82 ft:
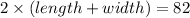
Now let us substitute the value of length from the first equation into the second equation. This gives,
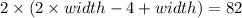
For convenience, let us represent the width by the letter w. This turns our equation into the following.
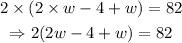
since 2w + w = 3w, the above becomes
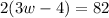
dividing both sides by 2 gives
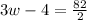
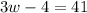
adding 4 to both sides gives
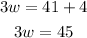
Finally, dividing both sides by 3 gives
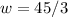
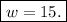
Hence, the width of the rectangle is 15 ft.
With the value of the width in hand, we now find the length of the rectangle.
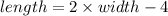
since width = 15, the above equation gives
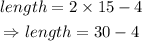
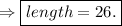
Hence, the length of the rectangle is 26 ft.
To summerise,
length = 26 ft
width = 26 ft