Question

Solve x2 – 7x = –13.

Answer 1

Answer: x =
`(7±i√(3))/(2)` (Ignore the A)

Step-by-step explanation: This is step-by-step using the QF (quadratic formula)

The first step is putting it into SF (Standard Form). Keep in mind the formula for SF is
`ax^(2)` ±
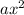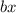`bx` ± c= 0.

You will want to move the -13 from the right side to the left by subtracting it.

x2 – 7x = –13

+13 +13 (in order to cancel out -13 you will need to use the

--------------------------- opposite operation, in this case adding it.) You will get

`x^(2)` - 7x + 13= 0 Now you want to use the QF, which is
`\frac{-b+/- \sqrt{b^(2) -4ac} }{2a}`

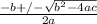
a = 1 (remember that
`x^(2)` has an invisible 1 in front of it) b = -7 (don"t forget any negative signs with the number(s)) c = 13

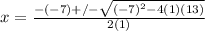`x=\frac{-(-7)+/-\sqrt{(-7)^(2)-4(1)(13) } }{2(1)}` Put everything in parenthesis to make it easier.

Use PEMDAS to solve. Start with
`(-7)^(2)`

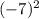
`x = (-(-7)+/-√(49-4(1)(13)) )/(2(1))` Now do all the multiplication under the square root first. Then the -(-7) and lastly the 2(1).

`x=(7+/-√(49-52) )/(2)` (1x13=13 and 4x13= 52) Now do the math in the square root.

`x=(7+/-√(-3) )/(2)` ---
`x=(7+/-√(-1)* √(3) )/(2)` ----
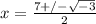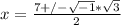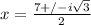`x=(7+/-i √(3) )/(2)` There's your answer.

Remember because
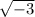`√(-3)` is not a real number it has to be broken down into
`√(-1) *√(3)`. -1 is = to i. i stands for imagiary.