Answer:
1653.426 meters.
Step-by-step explanation:
The diagram below represents the given problem:
The line of sight is the hypotenuse of the right triangle labeled x above.
Using trigonometric ratios:
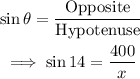
We solve for x:
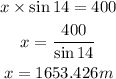
The line of sight distance from the television camera to the base of the stadium is 1653.426 meters.