Question

How can you tell when a quadratic equation has two identical, rational solutions?. a:when the radicand is negative. b:when the radicand is not a perfect square. c:when b in the quadratic formula is greater than the radicand. d:when the radicand equals zero

Answer 1

The quadratic equation has two identical, rational solutions:

d: when the radicand equals zero.

Explanation:

We know that the general quadratic equation of the type:

`ax^2+bx+c=0`

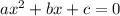
The solution is given by:

`x=(-b\pm √(D))/(2a)`

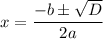
with discriminant:

`D=b^2-4ac`

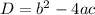
has:

• Two rational and identical solution if the radicand i.e.
  `D` is equal to zero.

• Two rational and unequal solution if the radicand i.e. D is strictly greater than zero.

• Two imaginary solution if the radicand i.e. D is strictly less than zero.

Answer 2

"When the radicand equals zero" is the one among the following choices given in the question that you can tell when a quadratic equation has two identical, rational solutions. The correct option among all the options that are given in the question is the fourth option or option "d". I hope the answer has helped you.