Question

Designer Dolls, Inc. found that the number N of dolls sold varies directly with their advertising budget A and inversely with the price P of each doll. The company sold 5200 dolls when $26,000 was spent on advertising and the price of a doll was set at $30. Determine the number of dolls sold when the amount spent on advertising is increased to $52,000. Round to the nearest whole number.. . A. 5,200 dolls. . B. 1,723 dolls. . C. 3,447 dolls. . D. 10,400 dolls

Answer 1

The correct answer among all the other choices is D. 10,400 dolls. This is the number of dolls sold when the amount spent on advertising is increased to $52,000. Thank you for posting your question. I hope that this answer helped you. Let me know if you need more help. 

Answer 2

D

Explanation:

Direct Variation takes the form
`A = kB`

Inverse Variation takes the form
`A=k((1)/(B))`

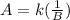
• Where A and B are the 2 variables associated and k is the proportionality constant.

Since number of dolls [N] varies directly with advertising budget [A], in our equation, A should go in the numerator and since number of dolls [N] varies inversely with price of dolls [P], P should go in the denominator.

Thus we can write our equation as:

`N=k((A)/(P))`

Solving this equation for k given the information "The company sold 5200 dolls when $26,000 was spent on advertising and the price of a doll was set at $30":

`N=k((A)/(P))\\5200=k((26,000)/(30))\\5200=k(866.67)\\k=(5200)/(866.67)=5.99`

Rounding
`k=5.99` to
`k=6`

Now, given that we want to find the number of dolls [N] when
`A=52,000` and
`P=30` , we have:

`N=(6)((52,000)/(30))\\N=10,400` dolls

Answer choice D is correct.