Question

A ball is thrown straight up into the air. The height, in feet, h(t), of the ball collected over t seconds is shown in the table.

Which statement is true?

The initial height of the ball is 96 feet.
The ball will hit the ground between 2 and 3 seconds after it was thrown.
The maximum height of the ball must be 96 feet.
The maximum height of the ball was 2.5 seconds after it was thrown.

Answer 1

Answer:The maximum height of the ball was 2.5 seconds after it was thrown.

the answer is D

Answer 2

Option D is correct

The maximum height of the ball was 2.5 seconds after it was thrown.

Explanation:

let a and b are the zeros of the function f(x) then;

f(x)= k(x-a)(x-b)

where, k is the coefficient.

As per the statement:

A ball is thrown straight up into the air. The height, in feet, h(t), of the ball collected over t seconds is shown in the table.

From the given table:

At t = 0

h(0)= 0

At t = 5

h(5) = 0

⇒0 and 5 are the zeros the function h(t)

then by definition we have;

`h(t) = k(t-0)(t-5)`

⇒
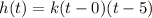
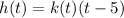`h(t) = k(t)(t-5)` .....[1]

Now substitute any point from the table i.e, (2, 96) in [1] to find k;

`96 = k(2)(2-5)`

`96 = k(2)(-3)`

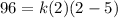
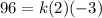
Simplify:

`96 = -6k`

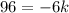
Divide both sides by -6 we have;

`-16 = k`

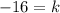
or

k = -16

then, we have the equation for h(t) as:

`h(t) = -16t(t-5)`

⇒
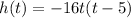
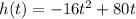`h(t) = -16t^2+80t` ....[1]

Initial height of the ball:

h(0) = 0

To find the maximum height of the ball.

A quadratic equation
`y=ax^2+bx+c`.....[2], the the axis of symmetry is given by:

`x = (-b)/(2a)`

On comparing [1] and [2] we have;

a =-16 and b = 80 then;

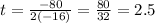`t = (-80)/(2(-16)) = (80)/(32) = 2.5` sec

⇒the maximum height of the ball was 2.5 second.

Therefore, the statement which is true is: The maximum height of the ball was 2.5 seconds after it was thrown.