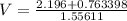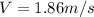Question

A 6.11-g bullet is moving horizontally with a velocity of 366 m/s, where the sign indicates that it is moving to the right (see part a of the drawing). The bullet is approaching two blocks resting on a horizontal frictionless surface. Air resistance is negligible. The bullet passes completely through the first block (an inelastic collision) and embeds itself in the second one, as indicated in part b. Note that both blocks are moving after the collision with the bullet. The mass of the first block is 1206 g, and its velocity is 0.662 m/s after the bullet passes through it. The mass of the second block is 1550 g. (a) What is the velocity of the second block after the bullet imbeds itself

Answer 1

`V=1.86m/s`

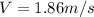
Step-by-step explanation:

Mass of bullet
`M_B=6.11g`

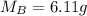
Velocity of bullet
`V_B=366m/s`

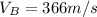
Mass of first block
`M_b_1=1206g`

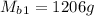
Velocity of block
`V_b=0.662m/s`

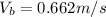
Mass of second block
`M_b_2=1550g`

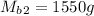
Generally the total momentum before collision is mathematically given as

`P_1=0.006kg*366+0+0`

`P_1=2.196kg\ m/s`

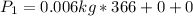
Generally the total momentum after collision is mathematically given as

`P_2=(1.206kg*0.633)+(1.550+0.00611)V`

`P_2=0.763398+1.55611V`

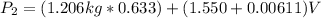
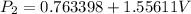
Generally the total momentum is mathematically given as

`P_1=P_2`

`2.196=0.763398+1.55611V`

`V=(2.196+0.763398)/(1.55611)`

`V=1.86m/s`