Question

Factor each trinomial. Then match the polynomial (term) on the left with its factored form (definition) on the right.

Match
Term
Definition

x2 – 4x – 12
x2 + 4x – 12
x2 – x – 12
x2 – 7x – 12

A) (x – 6)(x + 2)
B) Prime
C) (x – 2)(x + 6)
D) (x – 4)(x + 3)

Answer 1

x2 – 4x – 12 A) (x – 6)(x + 2) x2 + 4x – 12 B) Prime x2 – x – 12 C) (x – 4)(x + 3) x2 – 7x – 12 D) (x – 2)(x + 6) i think this is the awnser:)

Answer 2

`x^2-4x-12\ ------------------\ (x+2)(x-6)\\\\x^2+4x-12\ -----------------\ (x-2)(x+6)\\\\x^2-x-12\ -------------------\ (x-4)(x+3)\\\\x^2-7x-12\ ------------------\ Prime`

Explanation:

1)

`x^2-4x-12`

This could be factored by using the method of splitting the middle term.

i.e.

`x^2-4x-12=x^2-6x+2x-12\\\\i.e.\\\\x^2-4x-12=x(x-6)+2(x-6)\\\\i.e.\\\\x^2-4x-12=(x+2)(x-6)`

2)

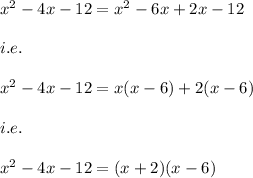
`x^2+4x-12`

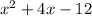
This could again be factored by the method of splitting the middle term as follows:

`x^2+4x-12=x^2+6x-2x-12\\\\i.e.\\\\x^2+4x-12=x(x+6)-2(x+6)\\\\i.e.\\\\x^2+4x-12=(x-2)(x+6)`

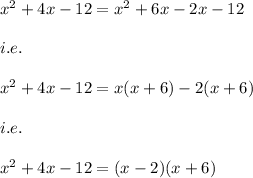
3)

`x^2-x-12`

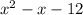
This could be factored by using the method of splitting the middle term.

i.e.

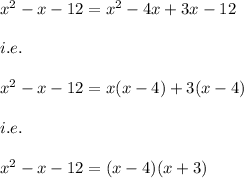
`x^2-x-12=x^2-4x+3x-12\\\\i.e.\\\\x^2-x-12=x(x-4)+3(x-4)\\\\i.e.\\\\x^2-x-12=(x-4)(x+3)`

4)

`x^2-7x-12`

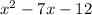
This polynomial could not be factored.

Hence, it is a prime expression.