Answer:
Therefore, Verify.
Explanation:
Given : cot θ ∙ sec θ = csc θ
To find : Verify the identity.
Solution : We have given
cot θ ∙ sec θ = csc θ
By the trigonometric identity : cot θ =
 .
.
sec θ =
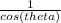 .
.
Then ,
Taking left hand side
cot θ ∙ sec θ
 *
*
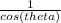
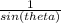
csc θ = right hand side.
Hence verify.
Therefore, Verify.