Question

What is the length of side PQ in this figure?

A.4
B.14
C. square root of 52
D.square root of 61

Answer 1

I hope this helps you

Answer 2

option: C

Explanation:

To find the side PQ ; we need to first find the length of the given line segment which is perpendicular to side PR; let name it as QS.

Now as ΔQSR is an right angled triangle.

and the length of the side QR and SR is given , so using Pythagorean theorem we have

`QR^(2)=SR^(2)+QS^(2)`

`5^(2)=3^(2)+QS^(2)\\ \\QS^(2)=5^(2)-3^(2)\\\\QS^(2)=25-3=16=4^2`

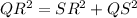
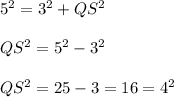
⇒ QS=4

Now again ΔQSP is an right angled triangle; so using Pythagorean theorem in ΔQSP we have

`PQ^(2)=QS^(2)+PS^(2)\\ \\PQ^(2)=4^(2)+6^(2)=16+36=52`

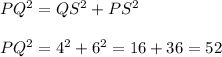
This means
`QS=√(52)=2√(13)`

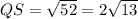
Hence, the length of side PQ is
`√(52)=2√(13)`.

Hence, option C is correct.