Question

A small rock falling from the top of a 124-ft-tall building with an initial downward velocity of –30 ft/sec is modeled by the equation h(t) = –16t2 – 30t + 124, where t is the time in seconds. For which interval of time does the rock remain in the air?

t = 2
t > –2
t < 2
t > 2


WHICH ONE?? D:

Answer 1

Third option is correct.

Explanation:

The given model is

`h(t)=-16t^2-30t+124`

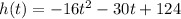
Where, h(t) is heigth of rock after time t (in seconds).

The initial height of rock is 124 ft.

The leading coefficient is negative. It means it is a downward parabola.

First we have to the x-intercepts of the function.

`0=-16t^2-30t+124`

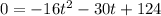
Using quadratic formula, we get

`t=(-(-30)\pm √((-30)^2-4(124)(-16)))/(2(-16))`

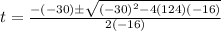
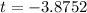`t=-3.8752` and
`t=2`

It means rock remains in the air between
`-3.875<t<2`.

The value of t can not be negative, therefore rock remains in the air between
`0<t<2`.

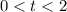Third option is correct.