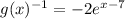Given the function
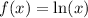
a) When we multiply the parent function by –1, we get a reflection about the x-axis. Then
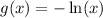
And three times as tall means 3 units up
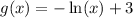
Shifted four units to the left means shifted 4 units left
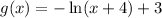
Answer: the new function is: g(x) = - ln(x+4) + 3
b) When we multiply the input by –1, we get a reflection about the y-axis.
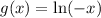
Shifted seven units up
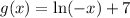
Half as wide means 1/2 f(x)
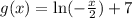
Answer: the new function is:
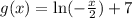
c) We find the inverse of
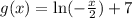
Then by definition of inverses, g(x) = y
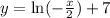
Next, replace all x’s with and all y’s with x
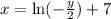
Now, solve for y
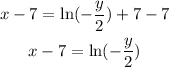
Apply properties of logarithms
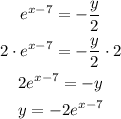
Answer: