Question

Given the parent function f(x)=ln(x)(a) Write a function whose graph has been reflected in the x-axis, is three times as tall, and has been shifted four units to the left.(b) Write a function whose graph has been reflected in the y-axis, has been shifted seven units up, and is half as wide.(c) Calculate the inverse function for your answer to question (b).

Answer 1

Given the function

`f(x)=\ln (x)`

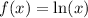
a) When we multiply the parent function by –1, we get a reflection about the x-axis. Then

`g(x)=-\ln (x)`

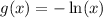
And three times as tall means 3 units up

`g(x)=-\ln (x)+3`

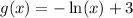
Shifted four units to the left means shifted 4 units left

`g(x)=-\ln (x+4)+3`

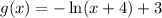
Answer: the new function is: g(x) = - ln(x+4) + 3

b) When we multiply the input by –1, we get a reflection about the y-axis.

`g(x)=\ln (-x)`

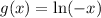
Shifted seven units up

`g(x)=\ln (-x)+7`

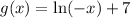
Half as wide means 1/2 f(x)

`g(x)=\ln (-(x)/(2))+7`

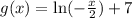
Answer: the new function is:

`g(x)=\ln (-(x)/(2))+7`

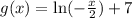
c) We find the inverse of

`g(x)=\ln (-(x)/(2))+7`

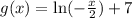
Then by definition of inverses, g(x) = y

`y=\ln (-(x)/(2))+7`

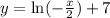
Next, replace all x’s with and all y’s with x

`x=\ln (-(y)/(2))+7`

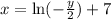
Now, solve for y

`\begin{gathered} x-7=\ln (-(y)/(2))+7-7 \\ x-7=\ln (-(y)/(2)) \end{gathered}`

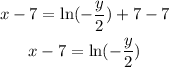
Apply properties of logarithms

`\begin{gathered} e^(x-7)=-(y)/(2) \\ 2\cdot e^(x-7)=-(y)/(2)\cdot2 \\ 2e^(x-7)=-y \\ y=-2e^(x-7) \end{gathered}`

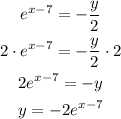
Answer:

`g(x)^(-1)=-2e^(x-7)`