Question

While fishing, you get bored and start to swing a sinker weight around in a circle below you on a 0.25-m piece of fishing line. The weight makes a complete circle every 0.50s, what is the angle that the fishing line makes with the vertical?

Answer 1

Answer: The correct answer is 75.6 degree.

Step-by-step explanation:

Calculate the angular velocity.

`\omega =(2\pi )/(T)`

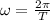
Here, T is the time.

Put T=0.50 s.

`\omega =(2\pi )/(0.50)`

`\omega =12.6\ rad\ per\ second`

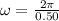
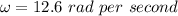
If T is the tension acting on the sinker then tension equals to the centripetal force due to the circular motion as the sinker is moving in the circular motion.

`T=mL\omega ^(2)`

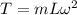
Here, m is the mass of the sinker and L is the length of the sinker.

By resolving the components of the tension, the vertical component of the tension equals to the weight of the sinker.

`Tcos\theta =mg`

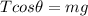
Calculate the angle that the fishing line makes with the vertical.

`cos\theta =(mg)/(T)`

`\theta =cos^(-1)((mg)/(T))`

Put
`T=mL\omega ^(2)`.

`\theta =cos^(-1)((g)/(L\omega ^(2)))`

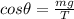
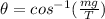
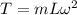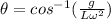
Put L= 0.25 , g= 9.8 meter per second and
`\omega =12.6\ rad\ per\ second`.

`\theta =cos^(-1)((9.8)/((0.25)\(12.6) ^(2)))`

`\theta =cos^(-1)(0.25)`

`\theta =1.32`

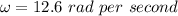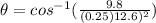
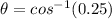
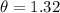
Convert radian into degree by multiplying 57.3 degree.

`\theta =75.6`

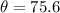
Therefore, the angle that the fishing line makes with the vertical is 75.6 degree.

Answer 2

Centripetal acceleration (Ac)

= (1/2)v^2/r^2

Gravity = 9.8

Angle with vertical tan = tan ^-1 (Ac/g)

You will get that the answer will be 76.1

Hope this helps