Question

A liquid vessel which is initially empty is in the form of an inverted regular hexagonal pyramid of altitude 25 feet and base edge 10 feet. By how much will the surface rise when 6,779 liters of water is added?

Answer 1

`\text{Surface area } = 265.14\ ft^2`

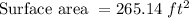
Explanation:

A liquid vessel in the form of an inverted regular hexagonal pyramid.

Altitude of pyramid, h = 25 feet

Base edge of pyramid, a = 10 feet

`\text{Volume of Pyramid}=(√(3))/(2)a^2h`

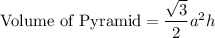
A liquid vessel contain maximum volume
`=(√(3))/(2)\cdot 10^2\cdot 25=2165\ ft^3`

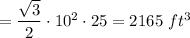
Change cubic foot to liter

`1\ ft^3 = 28.32\ liter`

`2165\ ft^3 = 61307.67\ liters`

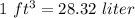
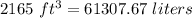
A vessel fill 6,779 liters of water.

6779 lt = 239.398 ft³

Therefore,
`239.398=(√(3))/(2)\cdot 10^2h`

`h=2.764\ ft`

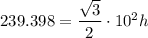
Surface area rise, a = 10 ft , h = 2.764 ft

`\text{Surface area } = 3a\sqrt{h^2+(3a^2)/(4)}`

`\text{Surface area } = 3\cdot 10\sqrt{1.764^2+(3\cdot 10^2)/(4)}`

`\text{Surface area } = 265.14\ ft^2`

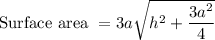
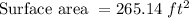
Hence, The surface rise when 6,779 liters of water is added to vessel will be 265.14 ft^2

Answer 2

Since: v =sqrt(3)/2 s^2h

6779 liters x 0.0353cu ft/1 liter= 239.299 cu ft
but by proportion s/h = 10/25
s = 10/25 h
and v = sqrt(3)/2 (10/25 h)^2 h
239.299 = 0.139 h^3

h = (239.299/0.139)^(1/3) = 11.985 ft