Answer:
y=5x-17
Explanation:
Given the equation of the line: y=5x+7.
We want to find a line parallel to it that passes through (4,3).
Slopes are used to determine if two lines are parallel or not.
First, we determine the slope of y=5x+7 with the slope-intercept form of a line.
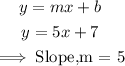
Two lines are parallel if they have the same slope.
• Therefore, the slope of the new line = 5
Since the two lines are parallel, the new line has the following properties:
• Slope, m =5
,
• Point, (x1,y1)=(4,3)
We then use these to find the required equation of the line.
Substitute the slope and point into the point-slope form of a line.
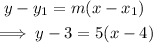
We then rewrite it in the slope-intercept form.
![\begin{gathered} \text{Open the bracket} \\ y-3=5x-20 \\ Add\text{ 3 to both sides} \\ y-3+3=5x-20+3 \\ y=5x-17 \end{gathered}]()
The required equation of the line is y=5x-17.