Question

A curve has the equation y = x^3 + 3x^2 − 16x + 2. a) Find an equation of the tangent to the curve at the point P (2, −10). Ive done that part and got it right. Then it says The tangent to the curve at the point Q is parallel to the tangent at the point P. b Find the coordinates of the point Q. Im so confused as to how its (-4,50) for point q. could someone please explain?

Answer 1

The equation of the tangent to the curve at the point P(2, -10) is:
y = 8x - 26

`f(x)=x^(3)+3x^(2)-16x`

`f'(x)=3x^(2)+6x-16`

`f'(2)=12+12-16=8`
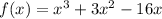
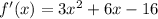
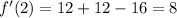
We need to find the coordinates of point Q where the slope of the tangent to the curve f(x) must also be 8.

`f'(x)=3x^(2)+6x-16=8`
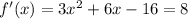
Now we have a quadratic:

`3x^(2)+6x-16-8=0`
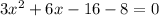
which simplifies to:

`x^(2)+2x-8=0`
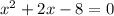
which factorizes to:(x + 4)(x - 2) = 0
Therefore x = -4, 2.
f(-4) = 48
Therefore the coordinates of Q are (-4, 48).