Question

Find the measure of the smallestangle in a triangle whose sidelengths are 4 m, 7 m, and 8 m.Recall the smallest angle isacross from the smallest side.

Answer 1

Given:

The sides of the triangle are given as,

`\begin{gathered} a\text{ = 4 m} \\ b\text{ = 7 m} \\ c\text{ = 8 m} \end{gathered}`

Required:

The smallest angle in a given triangle.

Step-by-step explanation:

The smallest angle lie across the smallest side.

By using cosine rule,

`a^2\text{ = b}^2+c^2-2bc.cos(\alpha)`

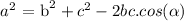
Substituting the values in the given expression,

`\begin{gathered} 4^2\text{ = 7}^2+8^2-2*7*8* cos(\alpha) \\ 16\text{ = 49 + 64 - 112cos\lparen}\alpha) \\ 16\text{ = 113-112cos\lparen}\alpha) \\ \end{gathered}`

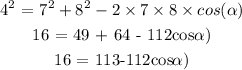
Calculating the value of the smallest angle,

`\begin{gathered} 112cos(\alpha)\text{ = 113-16} \\ 112cos(\alpha)\text{ = 97} \\ cos(\alpha)\text{ = }(97)/(112) \\ cos(\alpha)\text{ = 0.8661} \\ \alpha=\text{ cos}^(-1)(0.8661) \\ \alpha\text{ = 29.99}\approx\text{ 30} \end{gathered}`

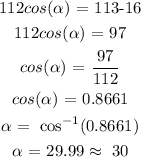
Answer:

Thus the measure of the smallest angle is 30 degrees.