Given:
The sides of the triangle are given as,

Required:
The smallest angle in a given triangle.
Step-by-step explanation:
The smallest angle lie across the smallest side.
By using cosine rule,
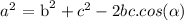
Substituting the values in the given expression,
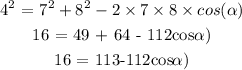
Calculating the value of the smallest angle,
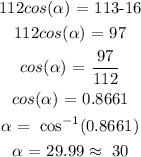
Answer:
Thus the measure of the smallest angle is 30 degrees.