Question

Write a linear equation, in slope intercept form to find the temperature t at elevation be on the mountain, where e is in thousands of feet.

Answer 1

13)T=-4.5e+103

14)when the elevation is 20000 ft, the temperature is 13 °

Step-by-step explanation

Step 1

set the points

so, let

`\begin{gathered} x-\text{axis (heigth)} \\ y-\text{axis (temperature)} \end{gathered}`

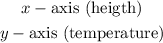
hence,

6000 ft= 6 thousands ft

12000 ft=12 thousands ft

P1(6,76)

P2(12,49)

Step 2

find the slope of the line:

the slope of the lines is given by the expression

`\begin{gathered} \text{slope}=\frac{\text{ change in y}}{\text{change in x}}=(y_2-y_1)/(x_2-x_(\square)) \\ \text{where} \\ P1(x_1,y_1) \\ \text{and } \\ P2(x_2,y_2) \\ \text{are two points from the line} \end{gathered}`

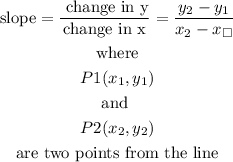
replace with P1 and P2 from the previous step

`\begin{gathered} \text{slope}=(y_2-y_1)/(x_2-x_1) \\ \text{slope}=(49-76)/(12-6)=-4.5 \end{gathered}`

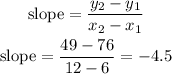
therefore, the slope is -4.5

Step 3

finally, get the equation

we can use the point-slope form and the, isolate y

so

`\begin{gathered} y-y_1=m(x-x_1) \\ \text{where m is the slope} \\ \text{and} \\ P1(x_1,y_1)\text{ is a point of the line} \end{gathered}`

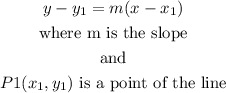
then ,let

P1(6,76)

slope=-4.5

replace

`\begin{gathered} y-y_1=m(x-x_1) \\ y-76=-4.5(x-6) \\ y-76=-4.5x+27 \\ \text{add 76 in both sides} \\ y-76+76=-4.5x+27+76 \\ y=-4.5x+103 \\ \end{gathered}`

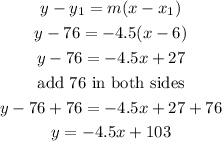
therefore, using T as the temperature and e as the elevation, we have

T=-4.5e+103

Step 4

(14)

now, we have to predict the temperature when the elevation is 20000 ft

so

let

e=20 thousand ft

T=?

replace in the equation we found

`\begin{gathered} T=-4.5(20)+103 \\ T=-4.5(20)+103 \\ T=-90+103 \\ T=13 \end{gathered}`

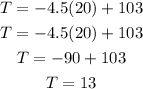
therefore, when the elevation is 20000 ft, the temperature is 13 °

I hope this helps you