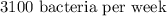Question

All you need is in the photo please answer fast please helpppppp

Answer 1

The average rate of change for the first five weeks of population growth is;

`3100\text{ bacteria per week}`

Step-by-step explanation:

Given that the growth of a population can be modeled by the exponential function;

`P(t)=500.2^t`

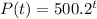
The average rate of change for the first five weeks can be calculated using the formula;

`m=(P(b)-P(a))/(b-a)`

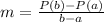
For the first five weeks;

`\begin{gathered} a=0 \\ b=5 \end{gathered}`

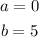
substituting to get the value of the function at this points;

`\begin{gathered} P(t)=500\cdot2^t \\ P(0)=500\cdot2^0=500\cdot1 \\ P(0)=500 \end{gathered}`
`\begin{gathered} P(t)=500\cdot2^t \\ P(5)=500\cdot2^5=500\cdot32 \\ P(5)=16000 \end{gathered}`

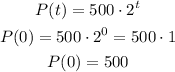
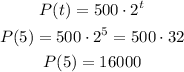
So, the average rate of change is;

`\begin{gathered} m=(16000-500)/(5-0) \\ m=(15500)/(5) \\ m=3100 \end{gathered}`

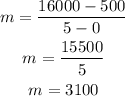
Therefore, the average rate of change for the first five weeks of population growth is;

`3100\text{ bacteria per week}`