Question

A distribution of measurements is relatively mound-shaped with a mean of 40 and a standard deviation of 15. Use this information to find the proportion of measurements in the given interval. between 25 and 55

Answer 1

The proportion of measurements between 25 and 55

P( 25 ≤ X≤ 55) = 0.6826

Explanation:

Step(i):-

Given that the mean of the Population = 40

Given that standard deviation of the Population = 15

Let 'x' be the random variable in normal distribution

Let 'X' = 25

`Z = (x-mean)/(S.D) = (25-40)/(15) = -1`

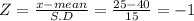
Let 'X' = 55

`Z = (x-mean)/(S.D) = (55-40)/(15) = 1`

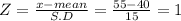
Step(ii):-

The probability that between 25 and 55

P( 25 ≤ X≤ 55) = P( -1≤z≤1)

= A(1) - A(-1)

= A(1) + A(1)

= 2 × A(1)

= 2× 0.3413

= 0.6826

The proportion of measurements between 25 and 55

P( 25 ≤ X≤ 55) = 0.6826

Final answer:-

The proportion of measurements between 25 and 55

P( 25 ≤ X≤ 55) = 0.6826