Question

The harmonic motion function d(t) = 4cos(3 t ), in which d is measured in centimeters and t is measured in seconds, gives the distance a swinging pendulum is from its resting position at time t. How far was the pendulum from its resting position when the motion began? What is the period of the pendulum's motion? How far is the pendulum from its resting position after 4.5 seconds?

Answer 1

• Distance when the motion began:, 4 cm

,

• Period: ,2π/3 sec

,

• Distance at t = 4.5 s:, 2.38 cm

Step-by-step explanation

When the motion begins, we usually set t = 0,

`d(0)=4\cos (3\cdot0)=4\cos (0)=4\cdot1=4`

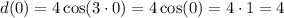
Hence, when the motion began, the pendulum was at 4 centimeters from the resting position.

The period of a sine or cosine function is given by 2π divided by the coefficient of t,

`T=(2\pi)/(3)`

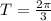
Hence, the period of the pendulum's motion is 2π/3 seconds.

Now, we have to find d(4.5) - remember to use your calculator in radians for this problem,

`d(4.5)=4\cdot\cos (3\cdot4.5)\approx2.38`

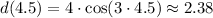
Hence, after 4.5 seconds the pendulum is at 2.38 centimeters from the resting position.