Given the quadratic equation:
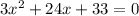
Dividing this equation by 3:
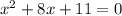
The general solution, given by the quadratic formula, is:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/pxvjqgmokhpuiark1x2l.png)
From the equation, we identify:
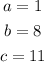
Now, we analyze the term inside the square root:
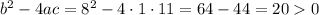
Since this term is positive, then the solutions are real.
Answer: C. 2 real solutions