Question

Hamburgers cost $2.50 and cheeseburgers cost $3.50 at a snack bar. Ben has sold no more than $30 worth of hamburgers and cheeseburgers in the first hour of business. Let x represent the number of hamburgers and y represent the number of cheeseburgers. The inequality 2.50x + 3.50y ≤ 30 represents the food sales in the first hour.

If Ben has sold 4 cheeseburgers, what is the maximum value of hamburgers Ben could have sold?

Answer 1

The maximum value of hamburgers is
`6`

Explanation:

Let

x-------> the number of hamburgers

y-----> the number of cheeseburgers

we know that

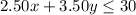`2.50x+3.50y\leq 30` -------> inequality that represent the situation

For
`y=4`

substitute in the inequality and solve for x

`2.50x+3.50(4)\leq 30`

`2.50x+14\leq 30`

`2.50x\leq 30-14`

`2.50x\leq 16`

`x\leq 6.4`

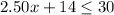
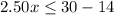
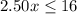
so

The maximum value of hamburgers is
`6`

Answer 2

Using the inequality
2.50x + 3.50y ≤ 30
substituting y with the number of cheeseburgers sold
2.5x + 3.5(4) ≤ 30
x = 6.4
The maximum number of hamburgers he can sell is 6