Question

Use mathematical induction to prove the statement is true for all positive integers n. The integer n3 + 2n is divisible by 3 for every positive integer n.

Answer 1

We have to use the mathematical induction to prove the statement is true for all positive integers n.

The integer
`n^3+2n` is divisible by 3 for every positive integer n.

• for n=1

`n^3+2n=1+2=3` is divisible by 3.

Hence, the statement holds true for n=1.

• Let us assume that the statement holds true for n=k.

i.e.
`k^3+2k` is divisible by 3.---------(2)

• Now we will prove that the statement is true for n=k+1.

i.e.
`(k+1)^3+2(k+1)` is divisible by 3.

We know that:

`(k+1)^3=k^3+1+3k^2+3k`

and
`2(k+1)=2k+2`

Hence,

`(k+1)^3+2(k+1)=k^3+1+3k^2+3k+2k+2\\\\(k+1)^3+2(k+1)=(k^3+2k)+3k^2+3k+3=(k^3+2k)+3(k^2+k+1)`

As we know that:

`(k^3+2k)` was divisible as by using the second statement.

Also:

`3(k^2+k+1)` is divisible by 3.

Hence, the addition:

`(k^3+2k)+3(k^2+k+1)` is divisible by 3.

Hence, the statement holds true for n=k+1.

Hence by the mathematical induction it is proved that:

The integer
`n^3+2n` is divisible by 3 for every positive integer n.

Answer 2

1. prove it is true for n=1
2. assume n=k
3. prove that n=k+1 is true as well


so

1.

`(n^3+2n)/(3)`=

`(1^3+2(1))/(3)`=

`(1+2)/(3)`=1
we got a whole number, true


2.

`(k^3+2k)/(3)`
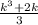
if everything clears, then it is divisble


3.

`((k+1)^3+2(k+1))/(3)` =

`((k+1)^3+2(k+1))/(3)` =

`(k^3+3k^2+3k+1+2k+2))/(3)`=

`(k^3+3k^2+5k+3))/(3)`
we know that if z is divisble by 3, then z+3 is divisble b 3
also, 3k/3=a whole number when k= a whole number


`(k^3+2k)/(3) + (3k^2+3k+3)/(3)`=

`(k^3+2k)/(3) + k^2+k+1`=
since the k²+k+1 part cleared, it is divisble by 3

we found that it simplified back to
`(k^3+2k)/(3)`

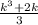
done