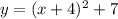Question

Suppose a parabola has vertex (–4, 7) and also passes through the point (–3, 8). Write the equation of the parabola in vertex form.

Answer 1

y=a(x-h)^2 +k
in the vertex (h, k) given that vertex (-4, 7)
we get y=(x-(-4))^2 +7
y=(x+4)^2 +7
hope it helps

Answer 2

The equation for a parabola can also be written in the "vertex form":

`y = a (x-h) ^ 2 + k`
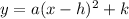
Where,
the vertex of the parabola is the point (h, k).
The value of a is the term that accompanies x ^ 2
Substituting values we have:

`y = a (x - (- 4)) ^ 2 + 7`
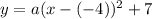
Rewriting we have:

`y = a (x + 4) ^ 2 + 7`
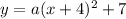
For the point (-3, 8) we have:

`8 = a (-3 + 4) ^ 2 + 7`
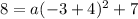
From here, we clear the value of a:

`8 = a (1) ^ 2 + 7 8 = a + 7 a = 8 - 7 a = 1`
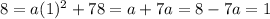
Then, the equation is given by:

`y = (x + 4) ^ 2 + 7`
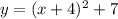Answer:
The equation of the parabola in vertex form is:

`y = (x + 4) ^ 2 + 7`