Answer:
A. 8.66 feet
B. 12.59 feet
C. Area of triangle when
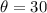 is 129.9 square feet. Area of triangle when
is 129.9 square feet. Area of triangle when
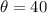 is 188.85 square feet. Increasing the angle
is 188.85 square feet. Increasing the angle
 increases the area.
increases the area.
Explanation:
The equation that models the height of the triangle is:

Where,
 is the height, and
is the height, and
 is the angle
is the angle
A.
When
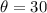 , the height is:
, the height is:
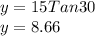
B. When
![\theta=40[/tex\ , the <strong>height</strong> is:</p><p>[tex]y=15Tan40\\y=12.59](https://img.qammunity.org/2017/formulas/mathematics/high-school/sb52l2w3rsubh2sxwhxci8ug9x9ksxwxca.png)
C. To find the area of the isosceles triangular shaped garden, we use the formula for the area of the triangle:
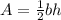
Where,
- A is the area
- b is the base, which is given as 30 feet, and
- h is the height [8.66 feet when the angle is 30 & 12.59 when angle is 40]
When Vance uses
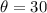 , the area is:
, the area is:
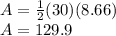 square feet
square feet
When Vance uses
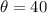 , the area is:
, the area is:
 square feet
square feet
So we see that when the angle is more, the area is also more.