Question

13. A catapult launches a boulder with an upward velocity of 148 ft/s. The height of the boulder (h) in feet after t seconds is given by the function h = –16t² + 148t + 30. How long does it take the boulder to reach its maximum height? What is the boulder’s maximum height? Round to the nearest hundredth, if necessary.

A) 9.25 s; 30 ft
B) 4.63 s; 640.5 ft
C) 4.63 s; 1,056.75 ft
D) 4.63 s; 372.25 ft

16. Solve the equation using the Zero Product Property.
(2x – 4)(2x – 1) = 0
A) 2, –1over2
B) 2, 1over2
C) –2, 2
D) –2, 1over2

Answer 1

13. Answer: The height will be maximum 372.25 ft at 4.63 s.

Step-by-step explanation:

Given that,

Upward velocity v = 148 ft/s

Function

`h = -16t^2+148t+30`.....(I)

On differentiate

`(dh)/(dt)=-32t+148`....(II)

for maximum height,

`(dh)/(dt)=0`

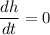
Put the value of
`(dh)/(dt)` in equation (II)

`-32t+148=0`

`t = (148)/(32)`

`t = 4.63\ s`

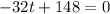
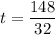
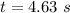
The maximum height is

Put the value of t in equation(I)

`h = -16*(4.63)^2+148*4.63+30`

`h = 372.25 ft`

Hence, The height will be maximum 372.25 ft at 4.63 s.

16. Answer: The value of x is 2,
`(1)/(2)`.

Step-by-step explanation:

Given that,

`(2x-4)(2x-1)=0`

Using zero product property

`2 x-4=0`

`x = 2`

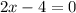
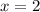
And,

`2x-1=0`

`x = (1)/(2)`

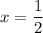
Hence, The value of x is 2,
`(1)/(2)`.

Answer 2

32t + 148 = 0148 = 32t4.625 = tt ≈ 4.63h = -16 • (4.625)^2 + 148 • 4.625 + 30 = 372.25
ANSWER: is D. 4.63 sec; 372.25 ft
2.) 2x - 4 = 0 and 2x - 1 = 0x = {4/2, ½}x = {2,½} ANSWER: is B 2, 1 over 2