Question

Suppose a laboratory has a 31 g sample of polonium-210. The half-life of polonium-210 is about 138 days. How many half-lives of polonium-210 occur in 966 days? How much polonium is in the sample 966 days later?

Answer 1

Answer : The amount of polonium in the sample 966 days later is, 0.24 g

Solution :

Polonium-210 is a radioactive element.

Formula used :

`N(t)=N_o* ((1)/(2))^{(t)/(t_(1/2))`

where,

`N(t)` = the amount of polonium-210 remaining after 't' days

`N_o` = the initial amount of polonium-210 = 31 g

t = time = 966 days

`t_(1/2)` = half-life of the polonium-210 = 138 days

Now put all the given values in the above formula, we get

`N(t)=(31g)* ((1)/(2))^{(966)/(138)}`

`N(t)=0.24g`

Therefore, the amount of polonium in the sample 966 days later is, 0.24 g

Answer 2

The answer is a) 7 half-lives and b) 0.78% (or as fraction 1/128) of the starting amount.

a) If half-life of Polonium-210 is 138 days, to calculate how many half-lives occur in 966 days, we will simply divide them: 966/138 = 7
So, 7 half-lives occur in 966 days.

b) To calculate the remaining amount, we will use the formula:

`(1/2)^(n) =x`
where n is the number of half-lives, and x is the remaining amount in decimals, and (1/2) is half-life.

We've already found that n = 7, so replace it in the formula:

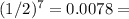
`(1/2)^(7) =0.0078 =` 0.78% = 1/128