Question

Write the expression as the sine, cosine, or tangent of an angle.

sin 9x cos x - cos 9x sin x

Answer 1

sin 8x

Explanation:

Answer 2

`\sin (8x)=\sin (9x) \cos (x) - \cos (9x)\sin (x)`

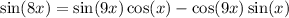
Explanation:

Given : Expression
`\sin (9x) \cos (x) - \cos (9x)\sin (x)`

To write : The given expression as the sine, cosine, or tangent of an angle?

Solution :

The given expression is in the form
`\sin A\cos B-\cos A \sin B`

Using trigonometric identity,

`\sin (A-B)=\sin A\cos B-\cos A \sin B`

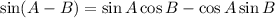
Substituting, A=9x , B=x

`\sin (9x-x)=\sin (9x) \cos (x) - \cos (9x)\sin (x)`

`\sin (8x)=\sin (9x) \cos (x) - \cos (9x)\sin (x)`

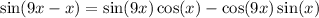
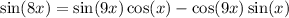
Therefore, The given expression is in the sin form sin(8x).