Question

Each roller under a conveyor belt has a radius of 0.5 meters. the rollers turn at a rate of 30 revolutions per minute. what is the linear velocity of the conveyor belt?

Answer 1

distance in a minute=0.5 times 30=15 meters
distance in a second=15 divided by 60=0.25 meters per second
hope it helps

Answer 2

The linear velocity of the conveyor belt is v=0.25 m/s.

Step-by-step explanation:

In a circular motion, the tangential velocity can be written as

`v_(t)=r\omega`

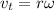
where r is the radius of the circle, and ω is the angular velocity.

In this case, we were given some data: the radius r=0.5 meters, and the revolutions per minute of the rollers. The first thing we have to do is to calculate ω with the proper units, which is rad/second, using the given revolutions per minute, so

`\omega=30(rev)/(min)*(2\pi rad)/(1rev)*(1 min)/(60 s)=\pi (rad)/(s)`

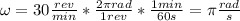
because in 1 minute, there are 60 seconds, and in 1 revolution, there are 2π rad.

Now, we can calculate the answer:

`v_(t)=r\omega=(1)/(2)m*\pi (rad)/(s)=(1)/(2)m*(1)/(2)(1)/(s)=(1)/(4)(m)/(s)`

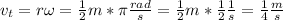
in which we had to convert rad/s to Hz (or 1/s), knowing that 2πrad=1Hz.

Therefore, the answer is v=0.25 m/s.