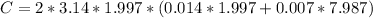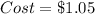Answer:
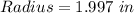 and
and
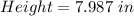
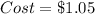
Explanation:
Given
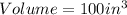
 -- Top and Bottom
-- Top and Bottom
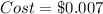 --- Sides
--- Sides
Required
What dimension of the cylinder minimizes the cost
The volume (V) of a cylinder is:
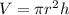
Substitute 100 for V
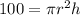
Make h the subject
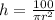
The surface area (A) of a cylinder is:
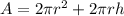
Where
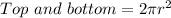
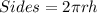
So, the cost of the surface area is:
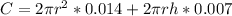


Substitute
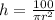
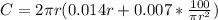
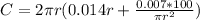
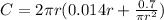
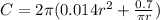
Open bracket
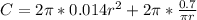
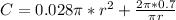
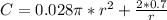

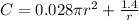
To minimize, we differentiate C w.r.t r and set the result to 0
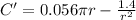
Set to 0

Collect Like Terms
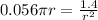
Cross Multiply

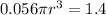
Make
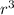 the subject
the subject
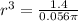


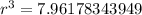
Take cube roots of both sides
![r= \sqrt[3]{7.96178343949}](https://img.qammunity.org/2022/formulas/mathematics/college/woknvhdi8emjonrzza4qlac7tbdnaatnm8.png)
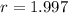
Recall that:
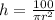
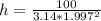
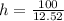
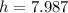
Hence, the dimensions that minimizes the cost are:
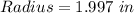 and
and
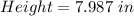
To calculate the cost, we have: