Solution
- In order for the quadrilateral to be a parallelogram, the opposite sides of the quadrilateral must be parallel and equal in length.
- Thus, we can say:
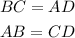
- This means we can equate the expression of BC to that of AD and the expression of AB to that of CD.
- Let us perform this operation below:

- Thus, let us solve these two equations simultaneously.
- We shall apply the substitution method.

Final Answer
The value of x is 9
The value of y is 4
-