The formula for Slope is m =
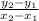
where m is the slope and the x's and y's are your given coordinates. So, plug the given information into the formula and solve for y.
m =
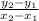
Plug in the given values
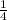
=
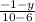
Cross multiply
10 - 6 = -4 - 4y Subtract
4 = -4 - 4y Add 4 to both sides
8 = -4y Divide both sides by -4
-2 = y Swich the sides to make it easier to read
y = -2
Check your answer by plugging -2 back into the equation with the other values.
[
tex] \frac{1}{4} [/tex] =
 Simplify the double negative
Simplify the double negative
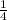 =
=
 Simplify the numerator and denominator
Simplify the numerator and denominator
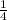 =
=
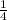
Since both sides equal each other, y = -2.